IoT Esp8266 Temperature and humidity sensor
This is my second project with the Esp-12-e module that contains the famous esp8266 from Espressif.
This sensor will connect to my Mqtt broker and send data to it. The broker will then with the help of Node red store it in an sqlite database and make some nice charts of it.
There are other similar sensor on the web, but I like to design and make my own. It’s my hobby and work.
The software will be writen with the Arduino ide for simple and quick design.
This is my second design now with Altium desiger. Switched from Eagle to Altium because Eagle has it’s limitation, not for this design but for more complexer. This board was not to difficult to start learning using Altium, and if I messed it up also not to expensive.
The hart of the board is the Esp-12-e module with a DHT22 Temperature and humidity sensor, all powered from a 16340 Li-ion battery that must last for at least a year. That’s what we hope.
The board contains also a ldo voltage regulator, led for debugging etc, some extra pads for “you never know in the future” and a programming socket. This socket is only used ones to program in the OTA and after that updating the firmware can be done over the air.
For now there’s nothing more to see then the 3D images from Altium Designer. Pcb’s are ordered in China and I have to wait for 2~4 weeks before they are here.
The picture is the panalized version, but the download version is a single board.
Update 3/10/2016:
Boards are in.
After some quick testing the esp8266 was not always starting up. My mistake, I forgot the pull-up resistor(12k) on gpio2.
The esp8266 determines with the help of gpio 0,2 and 15 how it will boot. With the gpio2 floating this gave problems.
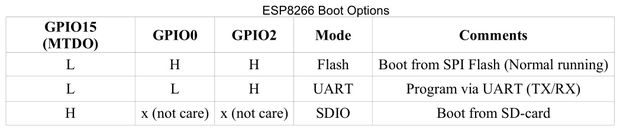
Added the pull-up resistor (R7) already to the Altium files below. If there are no more errors maybe I going order some new pcb’s.
Update 14/10/2016:
I wrote a small test program to test the hardware and get some numbers out and from it. You can find the test program on github.
Hardware is working fine. DHT22 (btw is official a AM2302, see source ) temperature reading is slightly different from my (also uncalibrated) temperature meter. 0.4 °C is more then the 0.2°C according the datasheet, but I’m not sure how accurate the temperature meter is.
Humidity is even harder to say if it’s correct because I don’t have anything to compare with.
Current consumption is around 27μA with a supply voltage of 3.6V.
Calculated is 10μA for the Esp8266 + 8μA for the battery measure voltage divider + 4μA for the LDO quiescent current = 22μA. Not bad result.
Because you can switch off the DHT22 completely by removing the power supply from it (gpio5) your not draining the additional 500μA standby current for this sensor. This will result in longer battery lifetime.
Update 7/10/2017:
Finally I got time to finish this project.
But what a disappointment, the battery on last for 1 day and we where hoping for a year 🙁 . Was sending every 30sec data to the mqtt broker and a collect and send data cycles from the esp8266 took 8 seconds.
So this made that the esp8266 120×8 seconds = 960 seconds = 16 minutes running every hour. 16min x 24 hours is 384 minutes. So the temperature and humidity sensor can run continue 384 minutes on a 3.6V Cr123a 1200mAh Li-io rechargeable battery. That’s not even that bad.
For longer battery life I optimized the code and reduced the data collect and send cycles time to 4 seconds. I’m now collecting the data during the periode that the wifi connection is setup, so that the total time that wifi is connected is reduced and with this the cycles time is down from 8 to 4.2 seconds.
I also changed the sample rate from 30sec to 5 minutes. This will bring down the running time 12×4.2 seconds=50 seconds every hour.
With this and a 2800mAh (Chinese specs) Cr123a battery that I ordered it should be possible to run 1 month from the battery, reducing the sample rate will even extend the battery life.
Pcb and battery where nicely fit in an Cr123a storage box, is no coincidence because the pcb was designed to fit in this box.
Update 11/03/2018:
It has been sometime ago with my last update.
What a drama with those Lithium-ion batteries, none of the batteries bought on ebay or Ali express have the capacity they promise. 1200mAh, 2800mAh forget it 250mAh is what you can get out of it. That’s why my first test with the sensor where that disappointed, if the battery only last 1/5 of the time promised 🙁
Bought now a Nitecore Li-Ion battery from Reichelt and now you know why this battery is 4x expensive then those from Ali-express, it was rated at 650mAh and after testing you could get 647mAh out of it, that’s better. The battery will last now for 1 month.
The second problem that occurs is that the DHT22 will stop working reliably below 3.3V. Bummer, the idea was that it should work down to 3.0V. Completely my fault and a bit of Adafruit. On there website was advertised that it works with 3.0V, however in the datasheet they talk about 3.3V, the rest of the internet (except those who copied Adafruit there text) are mentioning the 3.3V. Due this fault you can’t use a part of the battery charge because the sensor won’t work good.
With those problems in mind I decided to stop using the DHT22 and after some searching and reading the BME280 was the one the should do the job better. Have a look at this post to how this is going.
Altium 16 Design files V3











I am not able to write the firmware in the “Altium 16 Design files V3” project. I followed all the steps of the tutorial. Can you record without further trouble?
Hi Lucas,
The Altium design files doesn’t contain the firmware. Th altium files are the design files for the pcb.
You can find an example of the firmware on my github.